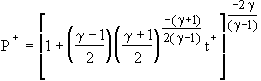(1)Experiments to Study the Gaseous Discharge and Filling of Vessels
J. CRAIG DUTTON
and ROBERT E.
COVERDILL
Department of Mechanical and Industrial Engineering,
University of Illinois at Urbana-Champaign Urbana, IL 61801, USA
ABSTRACT
Two experiments are described that have been developed to demonstrate the fundamentals of unsteady, compressible flow. The experiments involve the discharge of gas from a pressurized vessel and the filling of an initially evacuated vessel. The hardware, software, and procedures for the experiments are summarized. In addition, theoretical solutions for the entire vessel filling and discharge processes (choked and unchoked operation) are developed using both adiabatic and isothermal models of the processes. Example measurements from the discharge and filling experiments are presented and compared to the adiabatic and isothermal theories. The data are found to agree well with the theoretical predictions and follow the expected trends with respect to the rapidity of the processes.
Introduction
Experiments have been developed for the investigation of the discharge of compressed gas from a pressure vessel and the filling (charging) of an initially evacuated vessel. In each case the process occurs through a converging or converging-diverging nozzle. These experiments are used in a required senior-level course, "Thermal Science Laboratory," in the mechanical engineering curriculum at the University of Illinois at Urbana-Champaign. This course is taken after completion of the introductory thermodynamics, fluid mechanics, and heat transfer lecture courses and demonstrates, in a laboratory environment, the theories and concepts developed in the classroom. In other curricular arrangements, the experiments described here may also be used effectively in conjunction with an undergraduate fluid mechanics or thermodynamics course or with a first course in gas dynamics.
One of the objectives of these laboratory exercises is to perform unsteady, compressible flow experiments, thereby providing a complement to the more usual steady, incompressible flow problems that an undergraduate student investigates. In this context the experiments provide the opportunity to reinforce several compressible flow concepts, particularly the phenomenon of choking and differences in operation between converging and converging-diverging nozzles. In addition, the use of a digital data acquisition system based on a personal computer using graphical "object-oriented programming" software, pressure transducers, and thermocouples simplifies the collection of data, provides rapid graphical representation of the data on the computer monitor, and demonstrates the power and utility of ordinary desktop computers in a laboratory environment. The experiments are also relatively inexpensive to fabricate, and yield excellent, repeatable data that agree well with the theories developed for the vessel filling and discharge processes.
In addition to the usefulness of these experiments to engineering educators, the theoretical solutions that have been developed have found application in a variety of practical, industrial situations ranging from analysis of accident scenarios to prediction of the filling time of air bags and aircraft evacuation slides. We are unaware of any previous presentation of unified solutions for the entire vessel discharging or charging processes (i.e., both choked and unchoked operation). Such solutions, incorporating both adiabatic and isothermal models for the processes, are described briefly in the next section.
THEORETICAL DEVELOPMENT
Discharge analysis
The objectives of the analysis are to predict the pressure, temperature, and density of the gas in the tank and the mass flow rate out of the tank as functions of time during the discharge process. To accomplish these objectives the control volume shown in Fig. 1(a), which lies just inside the vessel walls, is used. In addition, the following assumptions are made:
- Properties of the gas in the tank are spatially uniform at any instant of time (i.e., quasi-steady or uniform state assumption);
- Average velocity of the gas in the tank is zero;
- Opening modeled as an ideal converging or converging-diverging nozzle with isentropic flow to the nozzle throat;
- One-dimensional flow and properties in the nozzle;
- Neglect gravitational potential energy;
- No shear or shaft work for the control volume;
- Gas is thermally and calorically perfect;
- Thermodynamic process is either adiabatic or isothermal.
The adiabatic assumption would be expected to be a good model for very rapid discharge processes in which case there would be little time for significant heat transfer between the tank walls and the gas. On the other hand, the isothermal assumption is expected to be appropriate for slow vessel discharge processes whereby there is sufficient time for heat transfer to maintain the temperature of the gas in the vessel constant.
Applying the integral continuity and energy equations to the control volume for the adiabatic case, the thermodynamic properties of the gas in the vessel can be shown to obey isentropic relations. In addition, for a large enough initial tank pressure Pi, compared to the back pressure PB, the nozzle will be choked during the initial portion of the discharge process. By starting with the integral continuity equation, substituting Fliegner's formula for the choked mass flow rate, and integrating the resulting ordinary differential equation, the solutions for the adiabatic and isothermal pressure-time histories in dimensionless form can be found as [1-3]
Choked Adiabatic Solution: 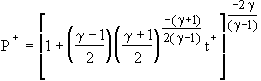(1)
Choked Isothermal Solution: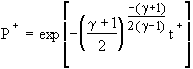 
(2)
In the discharge analysis the gas thermodynamic properties are
nondimensionalized with respect to their initial values so that 
in the expressions above. In addition, the
dimensionless time is defined as 
where the
characteristic time is given by 
. The symbols V, At, and ai denote
the vessel volume, nozzle throat area, and speed of sound of the
gas initially in the tank, respectively. In this dimensionless P+-t+
form, the pressure-time history of the gas in the vessel for both
models is therefore dependent only on the single parameter g, the gas specific heat ratio, as long as
the nozzle is choked.
As the tank pressure falls toward the back pressure, the
nozzle will eventually unchoke. The theoretical results can be
extended through the unchoked regime by writing a mass flow
expression at the nozzle exit plane, imposing the boundary
condition that the nozzle exit static pressure must equal the
ambient pressure, substituting this result into the integral
continuity equation, and integrating the resulting ordinary
differential equation using the unchoking point values 
as the initial condition [1]. To
our knowledge closed form solutions can only be obtained for t+ as an explicit function of P+, rather than vice versa, and only
for cases in which the gas specific heat ratio is the ratio of
integers, such as g=7/5 or 5/3. A
change of variables suggested by Owczarek [4]
has been used in the unchoked analysis. The results for the
adiabatic and isothermal models for g=7/5
are as follows:
Unchoked Adiabatic Solution:
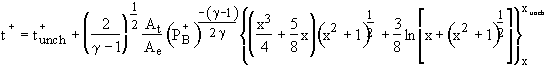(3)
Unchoked Isothermal Solution:
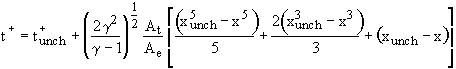(4)
where
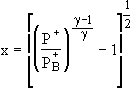(5)
The unchoked solutions are seen to depend on two additional
parameters as compared to the choked solutions: the nozzle
throat-to-exit area ratio 
and the dimensionless
back pressure 
. Also, note that these solutions can be
applied to the situation in which the entire vessel discharge is
unchoked. In that case, Eqs. (3)-(5) are used with 
replaced by unity and 
replaced
by zero.
Charge analysis
The objectives, control volume (Fig. 1(b)),
assumptions, and solution methods for the vessel filling analysis
are similar to those for the discharge analysis described above.
For the adiabatic model, however, the relations among the
thermodynamic properties are no longer isentropic. This result is
consistent with the fact that the kinetic energy of the gas
entering the tank must be dissipated if the average velocity in
the tank is zero. In the tank charging analysis, the
thermodynamic properties of the gas in the tank (whose initial
values are Pi, ri, and Ti) are normalized with respect to the
constant source values Ps, rs, and Ts, where atmosphere is used as the source and the
tank is initially evacuated in the experiments described below.
Thus, in the following expressions, the dimensionless pressure is
defined as 
, and the dimensionless time is given by where 
and as is
the speed of sound in the source gas. The adiabatic and
isothermal solutions for choked flow, which will occur if the
initial tank pressure is low enough compared to the source
pressure, are [2,5]
Choked Adiabatic Solution: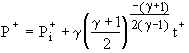 
(6)
Choked Isothermal Solution: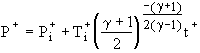 
(7)
The adiabatic choked P+-t+ solution is seen to depend on the
gas specific heat ratio g and the
initial pressure ratio 
. The isothermal solution for choked flow
depends on these two parameters plus the initial temperature
ratio 
.
For both choked solutions the pressure increase with time is linear,
but the rate of pressure increase for the isothermal case is
smaller by the factor 
.
As the pressure in the vessel approaches the source pressure, the nozzle will unchoke and the expressions above can no longer be used. Adopting a procedure similar to that described previously for the unchoked discharge analysis, but now setting the nozzle exit static pressure equal to the tank pressure for the unchoked case, yields the following results for unchoked vessel filling [5]
Unchoked Adiabatic Solution:
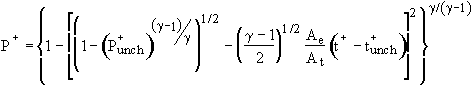(8)
Unchoked Isothermal Solution:
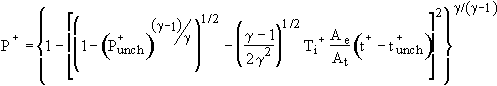(9)
Note that the two unchoked solutions are identical except that
the last term of the isothermal model is smaller than that for
the adiabatic model by the factor , which is similar to
the results for choked flow. The nozzle exit-to-throat area ratio
is also introduced as an additional parameter in both unchoked
solutions as compared to the choked flow results. It should be
noted that if these solutions are continued beyond the time at
which P+=1, the mass flow will
become negative (i.e., out of the tank) and the pressure
will decrease again, which is obviously physically unrealistic.
Thus, the solutions should be terminated at P+=1.
As was the case for the discharge analysis, the solutions given
above can be used for the situation in which the entire vessel
filling process is unchoked. In that case, the equations for the
unchoked regime are used with replaced by 
and replaced by zero.
In addition to the pressure-time history solutions presented above for the discharge and filling processes, similar time history expressions for the dimensionless density, temperature, and mass flow rate can also be developed from the thermodynamic relations that apply for the adiabatic and isothermal models. Further details about the theoretical analyses may be found in the laboratory manuals that have been developed for these experiments [1,5]; these manuals are available from the authors upon request.
EXPERIMENTAL EQUIPMENT AND METHODS
Apparatus
A schematic diagram of the apparatus for the discharge experiment is shown in Fig. 2. Two separate vessels are available; the smaller one has a volume of 4920 cm3 while the larger tank has a volume of 29,100 cm3. The vessels have several fittings, one each at the top and bottom and several on the sides. The lower and side ports are used, respectively, to mount a type T thermocouple, a pressure transducer [Sensotec 0-1.4 MPa(abs) strain gauge-type], a connection for pressurizing the tank, and a pressure relief valve. The upper port is the location at which a nozzle, either converging or converging-diverging, is mounted, and through which the gas discharge occurs. As shown in Table 1, six nozzles are available, ranging from 1.63 to 6.36 mm in throat diameter. A small flange fastened with socket head screws holds the nozzle securely to its seat while an O-ring is used to seal the nozzle against the seat. A flat-faced plug with an O-ring that is attached to a fast-acting toggle clamp seals tightly against the outer face of the nozzle when it is placed in the closed position.
A standard bottle of compressed air equipped with a regulator is used to pressurize the test vessel. A second regulator on a calibration stand is used to adjust the initial pressure in the vessel. A flexible hose with a quick-disconnect type of fitting couples the calibration stand to the vessel. A three-way valve on the test vessel stand (not shown) is used to allow air to flow into the vessel during charging, and also to isolate the vessel from the calibration stand when charging is complete. The third position of the valve can be used to vent the gas in the vessel to atmosphere. The pressure in the vessel is displayed on a Bourdon tube gauge on the calibration stand and is monitored during vessel charging until the pressure has reached the desired initial value, typically around 1 MPa. Since the pressure data are nondimensionalized with respect to this initial value, the actual starting pressure used is unimportant, as long as it is sufficiently high that the nozzle will be choked initially (the usual case of interest). As stated above, a thermocouple is situated in each of the vessels to monitor the temperature of the air. However, the thermocouples have neither been sized nor located to follow the transient behavior of the discharge process; the thermocouple data are used primarily to determine the initial gas temperature. Once the vessel is pressurized, the temperature of the air in the tank is allowed to return to the ambient value before discharging it through the nozzle. Discharge of the vessel occurs when the fast-acting toggle clamp is actuated, removing the sealing plug from the face of the nozzle.
Instrumentation
A computerized data acquisition system that allows for rapid collection of pressure, temperature, and time data has been developed for this experiment. The system consists of an Apple Macintosh computer with 8 MB of RAM, an Apple color monitor, a data acquisition card (ours is a multipurpose card purchased from National Instruments, model NB-MIO-16H), and LabVIEW 2 software, also from National Instruments. The signals that are input to the A/D card are the voltage outputs from the pressure transducer and the thermocouple that are located in the vessel. Since the time for complete discharge can last from a few seconds to several minutes depending on the vessel-nozzle combination being tested, the sampling interval of the LabVIEW application must be user selectable. This requires that the characteristic time tchar of the event be calculated, based on the tank and nozzle being investigated, to have a reasonably sized data set when completed (typically 50 data points are adequate). Since the A/D card is capable of greater than a 40 kHz sampling rate, this is an important step in the process. The sampling interval is entered in software from the "front panel" of the "virtual instrument" that is written in LabVIEW. A reproduction of the front panel for the discharge experiment is shown in Fig. 3. Displays of the pressure transducer output voltage and air temperature are included on the panel. In addition, the user may start, stop, or toggle between any of the three modes used to calibrate the transducer, monitor tank charging, or record data during the discharge.
After the process has ended, the data acquisition program is terminated and the raw voltage data from the pressure transducer are plotted versus time on the monitor by the LabVIEW program to verify that the event occurred properly (Fig. 3). The data are then saved to a spreadsheet file. Final data reduction is accomplished in a straightforward manner using the spreadsheet.
The apparatus and instrumentation for the vessel filling experiment are essentially identical to that described above for the discharge experiment. The only differences are that the compressed air bottle and calibration stand are replaced by a two-stage vacuum pump and a Bourdon tube absolute pressure gauge to monitor the tank pressure, and 0-140 kPa(abs) Sensotec strain gauge pressure transducers are used instead of 0-1.4 MPa(abs) transducers. In addition, the nozzles are installed with their rounded entrance section facing outward (rather than into the tank as for the discharge experiment).
EXAMPLE Results AND DISCUSSION
Example measurements and comparisons to theory will now be
presented for both the vessel discharge and filling experiments.
In all cases experimental uncertainties are specified in the
figure captions. These values have been determined using the
uncertainty propagation procedure outlined by Coleman and Steele
[6], together with the definitions of the
plotted dimensionless variables: 
and 
. As
discussed earlier, the reference conditions for the discharge
experiment are the initial values of the gas in the tank, while
for the charge problem they are the constant values of the source
gas. Estimates of the bias and precision limits to 95% confidence
have been made for each of the component quantities in the
definitions of the dimensionless quantities that are plotted.
Example vessel discharge results are shown in Fig. 4 where both the experimental data and the adiabatic and isothermal theories have been plotted. Figure 4(a) corresponds to the most rapid discharge possible with our hardware: the nozzle with the largest throat diameter mounted on the smaller tank (see Table 1 for nozzle dimensions and characteristic times). This discharge occurs in a little over 2 sec (approximately five characteristic times), and the data are seen to agree well with the adiabatic theoretical results for the entire duration of the process. At the other extreme is the smallest throat diameter nozzle used in conjunction with the large tank, Fig. 4(b). In this case the process requires about 200 sec. During the initial stages of the discharge, the data follow the adiabatic theory quite closely, as there is little time elapsed and only a small temperature difference between the gas and vessel walls, so that significant heat transfer does not occur. However, as the discharge proceeds, heat transfer does occur, the gas tends to remain at constant temperature, and the P+-t+ results more closely follow the isothermal theory. The thermocouple measurements, which are admittedly qualitative for the reasons discussed above, agree with this reasoning.
Figure 5 presents composite results for
two series of experiments that can be performed with this
hardware. In Fig. 5(a) the initial tank
pressure, and therefore , are held approximately
constant and several vessel-nozzle combinations are examined.
Although the characteristic times for the extreme cases differ by
nearly two orders of magnitude (Table 1), when plotted in this
dimensionless format, the data for all cases collapse to a fairly
narrow band about the adiabatic and isothermal theoretical
predictions. This result is pedagogically useful in reinforcing
dimensional analysis concepts. However, the trends described
above, that the faster discharges agree more closely with the
adiabatic theory while the slower ones agree better with the
isothermal theory, are also discernible in Fig.
5(a). Figure 5(b) shows the results of
a series of experiments in which the initial pressure, and
therefore 
, are varied for the same vessel-nozzle
combination. These experiments demonstrate that a single curve
describes the dimensionless pressure-time history for choked
flow, but that the unchoking point and the asymptotic value of P+
at long times depend on . Since the discharges
plotted in Fig. 5(b) are all relatively
fast ones, taking on the order of 10 sec or less, only the
adiabatic theory has been plotted to avoid clutter. The agreement
between the data and the theoretical predictions is excellent.
Results from typical vessel filling experiments are shown in Fig. 6. As was done for the discharge results, Fig. 6(a) presents data and predictions for the fastest charging experiment (approximately one second), while Fig. 6(b) does so for the slowest one (about 100 sec). Clearly, the agreement between the data in Fig. 6(b) for the slow charging process agree very closely with the isothermal theory. While the data in Fig. 6(a) for the fast filling process are shifted somewhat toward the prediction of the adiabatic model, they still lie closer to the isothermal prediction. This result can be explained by the observation that for vessel filling enhanced forced convective heat transfer occurs, compared to vessel discharge, due to jet impingement phenomena on the walls of the tank. In addition, the heat capacity of the tank walls is estimated to be more than an order of magnitude greater than that of the gas. Thus, even for rapid filling, substantial heat transfer between the gas and the vessel walls occurs and the gas temperature remains approximately constant. This hypothesis is again qualitatively confirmed by the thermocouple measurements.
Composite results for two series of experiments in which the
vessel-nozzle geometry and initial pressure ratio were varied are shown in Figs.
7(a) and 7(b), respectively. In Fig. 7(a)
the data for four vessel-nozzle combinations at an approximately
constant value of are seen to collapse
near the isothermal theory, although the expected trends with
experiment characteristic time can be discerned. Figure 7(b) presents results in which was varied for a given vessel and nozzle, including
the upper two curves for which the entire filling process was
unchoked. For this vessel and nozzle, the experiments require a
filling time of about 15 sec or less. In all cases the isothermal
theory, which is clearly the superior one for the cases
investigated here, is in close agreement with the data.
All of the experimental results presented here have been for cases in which converging nozzles were used. This is because these nozzles provide the extremes in the experimental characteristic times with the current equipment (Table 1). However, use of both the converging and converging-diverging nozzles illustrates the differences in choking characteristics of these two designs, in particular that the converging-diverging nozzles remain choked over a larger range of pressure ratios than do the converging nozzles.
SUMMARY AND CONCLUSIONS
Experiments to study the discharge of compressed gas from a pressure vessel and filling of an initially evacuated tank are described. Theoretical solutions for the two processes, incorporating both adiabatic and isothermal models, are also presented and compared to example measurements from the experiments. In each case, the agreement between the experimental data and theoretical predictions is found to be quite good.
In addition to demonstrating the accuracy of the one-dimensional theories developed here, these experiments can be used in open-ended experimental design situations. One possibility would be to introduce the students to the theoretical solutions and the available equipment and then ask them to design experiments that determine the range of parameters over which each model, adiabatic or isothermal, is the more accurate. Another possibility would be to pose an industrial application, such as a vessel discharge or filling accident scenario, for which the parameters (such as vessel size, opening area, initial pressure, or initial temperature) are far outside those that can be achieved in the laboratory. The students can then be asked to design experiments that answer questions concerning the time for vessel discharge or filling, the pressure, temperature, and mass flow time histories, etc. for the posed scenario. To answer these questions, the students obviously must identify the pertinent dimensionless variables, either by non-dimensionalizing the governing equations or by using the Buckingham Pi procedure, before proceeding with the experiments. Other open-ended experimental design experiences are also possible.
These experiments have been used in their current format for the last several years in a required senior-level thermal science laboratory course at the University of Illinois at Urbana-Champaign. In general, student feedback on the experiments is very positive. The experiments require substantial hands-on interaction, they make noise, and the students are particularly interested in the use of the digital data acquisition system and object-oriented LabVIEW programming language for acquiring the measurements. In addition, the data reduction is straightforward and is easily accomplished on a spreadsheet. Although safety is obviously a concern for the discharge experiment because of the use of compressed gas, the filling experiment is extremely safe since only subatmospheric pressures occur. In summary, it is our experience that these experiments are excellent vehicles for demonstrating the fundamentals of unsteady, compressible flow. In addition, the analytical solutions that have been developed for the charging and discharging processes are useful in a number of practical applications.
ACKNOWLEDGMENTS
We would like to acknowledge Christopher P. LaMothe for his help in developing the LabVIEW virtual instrument and in obtaining the example experimental results.
REFERENCES
TABLE AND FIGURE CAPTIONS
, (b) variable
and constant nozzle-tank combination; uncertainties same
as in Fig. 4., (b) variable
and constant nozzle-tank combination; uncertainties same
as in Fig. 6.